
- STRATIFIED SAMPLING LATIN HYPERCUBE SAMPLING SOFTWARE
- STRATIFIED SAMPLING LATIN HYPERCUBE SAMPLING CODE
Orthogonal sampling, by definition, produces the ideal sample in this regard (exactly zero correlation). From: Encyclopedia of Sustainable Technologies, 2017. See test/sudoku_cor_test.py to produce actual numbers. Latin hypercube sampling is one form of stratified sampling that can yield more precise estimates of the distribution functions than Monte Carlo. The improvement is the most marked in two dimensions (because sudoku LHS stratifies in 1 and N dimensions, and here N = 2), but some improvement is also noticeable for at least N = 3 and N = 4 (where stratification occurs only in 1 and 3 (resp. In the sense of the pairwise linear correlation coefficient of columns (which contain the permutations), sudoku LHS typically improves statistical independence when compared to pure Monte Carlo or classical LHS. Statistical independence of sample components IHS is (close to?) ideal in this regard, as it specifically aims to maximize the distance between pairs of sampled points. 1 and was further improved by Iman and Conover 2. Consider a multiple integral involving K random variables.

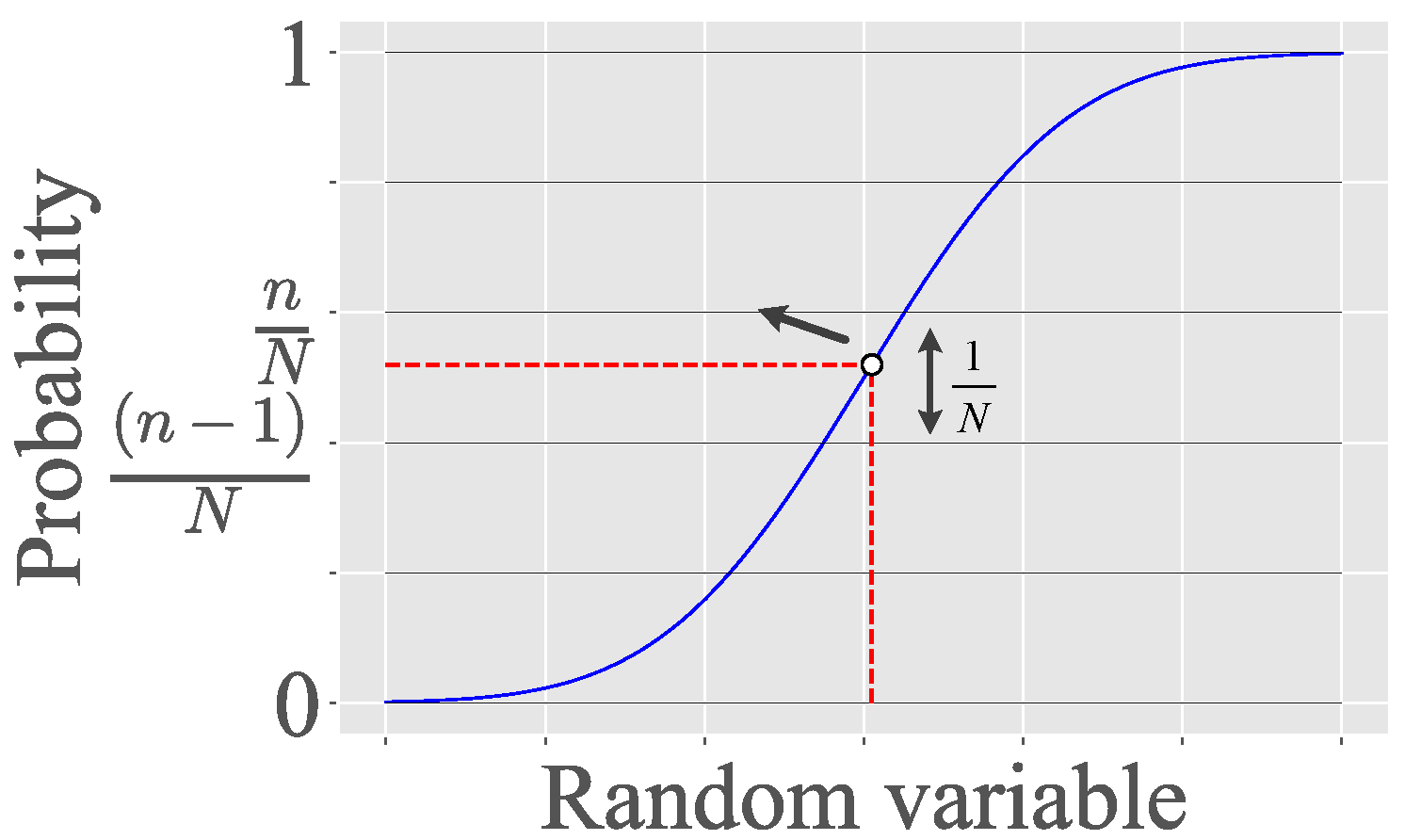
LHS is a popular stratified sampling technique which was first proposed by MacKay et. The advantage of stratified sampling over simple random sampling is that even though it is not purely random, it requires a smaller sample size to attain the. The Latin hypercube sampling (LHS) technique is a special method under the umbrella of stratified sampling that selects random samples of each random variable over its range in a stratified manner. In 43rd AIAA structures, structural dynamics, and materials conference. For this, a sampling technique called Latin Hypercube sampling (LHS) is selected and modified according to the objectives of the current research. Sudoku LHS improves on pure Monte Carlo and classical LHS, but loses to IHS, on which the original paper is: Comparison to other methods Stratification
A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Codeįor a quick description of classical LHS, see e.g. Latin hypercube sampling itself was first described in Ye 1998: Orthogonal column Latin hypercubes and their application in computer experiments Owen 1992: Orthogonal arrays for computer experiments, integration and visualization, Tang 1993: Orthogonal Array-Based Latin Hypercubes, The latter refers to LHS sampling using orthogonal arrays about that, see the articles: Sudoku LHS is inspired by, but not related to, orthogonal sampling.
STRATIFIED SAMPLING LATIN HYPERCUBE SAMPLING CODE
Details are provided in the source code comments. It uses a technique known as 'stratified sampling without replacement' ( Iman et al. Latin Hypercube sampling differs from Monte Carlo Sampling in that Latin Hypercube sampling asked in Business by JessME1. This paper develops asymptotically valid confidence intervals for quantiles that are estimated via simulation using LHS.
STRATIFIED SAMPLING LATIN HYPERCUBE SAMPLING SOFTWARE
In fact, we would say that it is one of the features that is essential in any risk analysis software package. Latin hypercube sampling (LHS) is a variance-reduction technique (VRT) that can be thought of as an extension of stratified sampling in multiple dimensions. the number of samples), and requires a linear amount of memory. Latin Hypercube sampling, or LHS, is an option that is now available for most risk analysis simulation software programs. The sudoku LHS algorithm is a bit like the first stage in the design of an N-dimensional sudoku puzzle, hence the name: each "sudoku box" must have exactly the same number of samples, and no two samples may occur on the same axis-aligned hyperplane. Graphical analysis for continuous data and chi-square analysis of categorical data suggested optimal sample size for this study area is approximately 200 to 300 (0.05–0.1%).Latin hypercube sampler with a sudoku-like constraint The cLHS code was run in Matlab™ (Mathworks, 2008) and statistical analysis was performed using the R statistical language (R Development Core Team, 2009). This paper briefly reviews cLHS and investigates different sample sizes for representing five environmental covariates in a 30,000-ha complex landscape in the Great Basin of southwestern Utah. As the smallest possible sample is important for efficient field work, what is the optimal sample size for digital soil mapping? An optimal sample size accurately represents the variability in the environmental covariates and provides enough samples for predictive models. Conditioned Latin Hypercube Sampling (cLHS) is a type of stratified random sampling that accurately represents the variability of environmental covariates in feature space.


 0 kommentar(er)
0 kommentar(er)
